Neutrinos come in three flavors, corresponding to the three types of charged leptons (electron, muon, and tau). It was once thought that, like photons, neutrinos had no mass. If true, this would imply that neutrinos don’t change flavor; if an electron neutrino was produced, then it could only ever interact as an electron neutrino, never as a muon or tau neutrino.
The first evidence that this model of neutrinos was incorrect came from the Homestake experiment in the late 1960’s, which aimed to measure the flux of electron neutrinos produced by nuclear reactions in the sun’s core. The detected flux was consistently much less than was predicted by the Standard Model, a discrepancy that would go unsolved for decades.

Eventually, with the advent of more sophisticated neutrino observatories such as Japan’s Super-Kamiokande and Canada’s Sudbury Neutrino Observatory in the late 1990’s, the answer was determined. The Homestake experiment was only able to detect electron neutrinos, while the new observatories were sensitive to interactions involving the other neutrino flavors. When the total neutrino flux was measured, it agreed with theoretical predictions, implying that electron neutrinos from the sun had changed flavor on their way to the observatories on Earth in a process that came to be called neutrino oscillation.
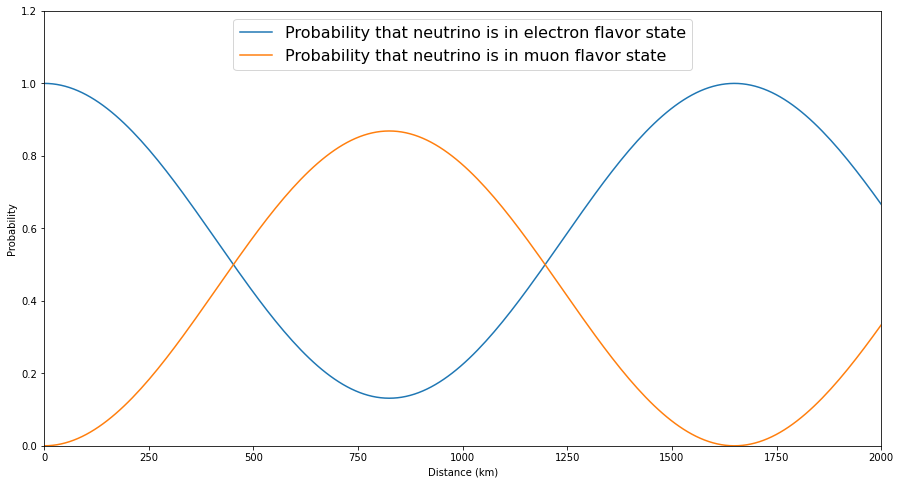
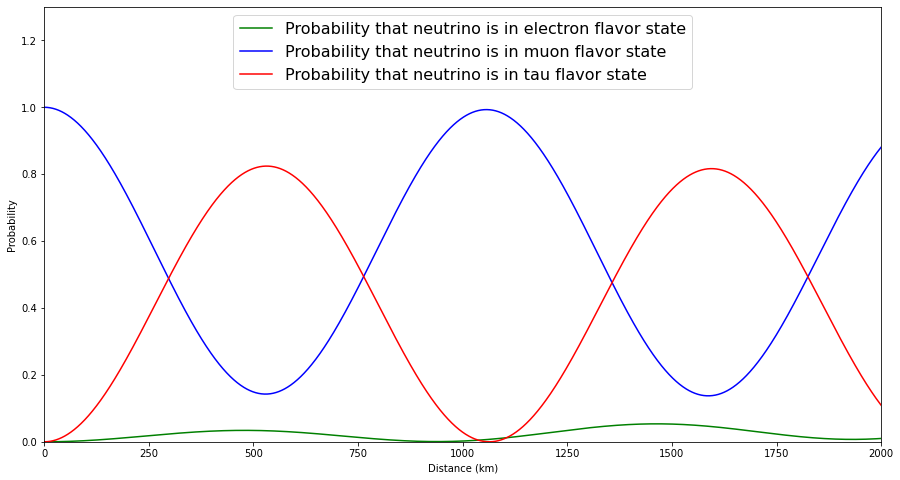
The experimental verification of neutrino oscillation implies that neutrinos do, in fact, have mass; however, the masses are so tiny as to be impossible to measure directly. In addition, for neutrino oscillation to occur, there must be mixing between states with definite flavor and states with definite mass. For example, when an electron neutrino is produced, it is in a state of definite flavor but not in a state of definite mass; rather, it is in a superposition of mass eigenstates. The details of how the mass eigenstates are mixed into the flavor eigenstates are encoded by several parameters known as mixing angles.
The mass eigenstates propagate through space with a frequency that depends on their mass: the larger the mass, the faster the frequency. Interference between these different frequencies causes neutrinos to oscillate between the different flavors as they travel. The probability that a neutrino is in a particular flavor state depends on a number of parameters, such as the initial flavor, the mixing angles, the energy of the neutrino, the distance traveled, and the differences between the squares of the masses. Click on one of the images to go to an interactive graph where you can see how these parameters change the shape of the probability curves!